Das grundsätzliche Leistungspotential des Abgases ergibt sich mit dem Integral der Enthalpie und dem Abgasmassenstrom.
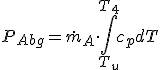
P_{Abg}=\dot{m}_A\cdot\int_{T_u}^{T_4} c_pdT
Das Integral befindet sich in den Grenzen von der Abgastemperatur T4 und der Umgebungstemperatur Tu . Das wäre also die maximale Leistung, die sich aus dem Abgas gewinnen lassen könnte. Die spezifische Wärmekapazität Cp ist abhängig von dem Arbeitsgas und der Temperatur. Das Abgas wird, in Ermangelung von Abgasmesstechnik und einer entsprechend gestalteten Simulation, vereinfacht als ideales Abgas behandelt. Bei der idealen Verbrennung entsteht nur CO2 und Wasserdampf. Zusätzlich ist noch nicht verbrannter Stickstoff N2 aus der Luft enthalten. Dafür wird dann, mittels der Gesetzmäßigkeiten für Gasgemische, die spezifische Wärmekapazität für das Abgas, in Abhängigkeit von der Temperatur T bestimmt.
![]()
c_p=a+b\cdot\left(\frac{T}{1000}\right)+c\cdot\left(\frac{T}{1000}\right)^2+d\cdot\left(\frac{T}{1000}\right)^3
Mit Hilfe des Cp - Wertes und der universellen Gaskonstante wird die spezifische Wärmekapazität Cv berechnet.
![]()
c_v=c_p - R
Der Quotient aus Cp und Cv ergibt den Isentropenexponenten κ :
![]()
\kappa=\frac{c_p}{c_v}
Den Abgasmassenstrom kann man auf unterschiedlichen Wegen bestimmen. Neben einer direkten Messung ist die handlichste Methode die Bestimmung aus der eingespritzten Kraftstoffmenge ṁκ und dem Verbrennungsluftverhältnis λ.
![]()
\dot{m}=\dot{m}_\kappa\cdot(\lambda\cdot\ l_{min}+1)
Da es technisch nicht sinnvoll umsetzbar ist, die Abgastemperatur bis auf die Umgebungstemperatur abzusenken, kann die Leistung des Abgases nicht vollständig ausgeschöpft werden.
Die Leistung, die sich mit der Turbine gewinnen lässt, berechnet sich basierend auf der thermodynamischen Zustandsänderung.
![]()
P_T=\dot{m}_AR_3T_3\frac{\kappa_3}{\kappa_3-1}\left[1-\left(\frac{p_4}{p_3}\right)^{\frac{\kappa_3-1}{\kappa_3}}\right]\cdot\eta_{T,is}
Die tatsächliche Leistung, die am Ende in Form von elektrischer Energie in einer Batterie verfügbar ist, ist nochmal um den elektrischen Wirkungsgrad ηel verringert. Er setzt sich aus Anteilen des Generators, der Leistungselektronik und dem Batterieladevorgang zusammen. Die Leistungsentnahme und die schlussendliche Nutzung für das Bordnetz oder einen elektrisch angetriebenen Verdichter müsste auch noch in der Betrachtung berücksichtigt werden. Das ist allerdings zum derzeitigen Zeitpunkt nicht sinnvoll bzw. nicht hinreichend genau möglich.
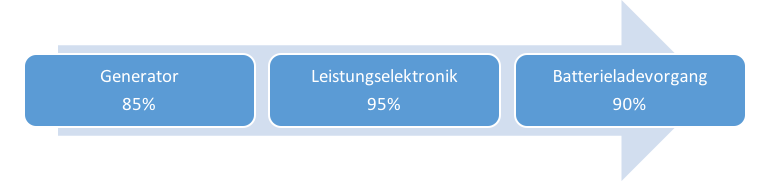
Die dargestellten Teilwirkungsgrade sind Schätzwerte basierend auf Erfahrungswerten aus der Praxis. Der Generator läuft mit einem eher mittelmäßigen Wirkungsgrad aufgrund der hohen Drehzahlen der Turbine. Die Leistungselektronik weist innerhalb der Schaltungen Verluste auf und der Ladevorgang für moderne Lithium Akkumulatoren hat einen Wirkungsgrad zwischen 90 und 95%.
In Summe beläuft sich der elektrische Wirkungsgrad auf rund 73%. Mit diesem werden dann die weiteren Betrachtungen durchgeführt.
Um schlussendlich eine Effizienzsteigerung feststellen zu können, muss der Nutzwirkungsgrad ηe betrachtet werden. Dieser berechnet sich aus der Nutzleistung Pe , der Kraftstoffmasse und dem Heizwert Hu des Kraftstoffs.
![]()
\eta_e=\frac{P_e}{m_k\cdot H_u}
Die Nutzleistung beschreibt dabei die Leistung, die tatsächlich noch genutzt werden kann. Es sind also sämtliche Verluste und Nebenverbraucher (Pumpen, Reibung, etc.) bereits abgezogen. Um die Vergleichbarkeit zum System mit einem turbinenbetriebenen Generator zu gewährleisten, wird nachträglich die elektrische Leistung des Seriengenerators zur Nutzleistung addiert, da diese sonst das Endergebnis verfälschen würde. Dementsprechend ist die Nutzleistung wie folgt definiert:
![]()
P_e=P_M+P_{el}
Den größeren Anteil an der Nutzleistung hat die Motorleistung PM. Die elektrische Leistung Pel steht sowohl für den Seriengenerator als auch für ein späteres System mit Abgasturbine. Wenn man eine Fallunterscheidung einführt, dann würde dies folgendermaßen aussehen:
![]()
Fall1: P_{el}=P_{Gen}
![]()
Fall2: P_{T}=\eta_{el}
Mit diesen jeweiligen elektrischen Leistungen und der Motorleistung aus dem Fahrprofil, kann dann schlussendlich ein Nutzwirkungsgradverlauf erstellt werden. Dieser wird dann im weiteren statistisch ausgewertet, um den möglichen Nutzen zu analysieren.